
A Practical Guide To Asymmetric Encryption - Part 1
Background
We want to cover things like why we need to secure information. What is encryption & decryption. How this can be achieved in theory. This is a 2 parts series & this is the 1st part wherein we would build up a strong foundation so that when you code in the 2nd part, you are confident of what you are doing.
Prerequisite
None for this. Anyone with or without coding background could easily follow this article. I would recommend you to read my previous article: Introduction To Blockchain & Cryptocurrency before or after reading this one.
Let me know if you have seen a movie called The Imitation Game, it is about Alan Turing, a British mathematician who joins the cryptography team to decipher the German enigma code.

We Need Encryption
Exchange of information happens every day via phone call, SMS, email, tweeting on Twitter, reading online articles like this one, etc. All of this has to be done in a secure channel. I would want you to read the information I have written as it is, what if someone intercepts this webpage before coming to your browser and changes the information? What if you are doing an online transaction to buy stuff and a hacker intercepts the network request & changes the price you pay midway! That is why we have some security protocols (set of rules) in place so things like the above can be prevented up to great extent.
One way or the another it is all encryption and hashing under the hood to protect "Exchange of Information". The information you send over the network is encrypted or digitally "signed" and then when it reaches the receiver, it is decrypted or digitally "verified" (checking the signature and its integrity). Hence if someone in between intercepts and peeks into it, he/she would not see actual information, just the cipher text.
Even now when you are reading this article in browser, you would see a lock icon beside the URL (on top left in Chrome) & when you click that, it would say "Connection is secure" in green. This ensures what you're reading right now is written by me and no one has intercepted & modified this article 🙂
I think now it is pretty clear why we need to keep information encrypted & why pretty much everything you surf on the internet is also made secure.
Symmetric & Asymmetric Encryption
There are two kinds of Encryption techniques at a broader level: Symmetric & Asymmetric Encryption. The contextual meaning of the English word Symmetric over here could be two things identical & completely in sync with each other. Asymmetric could mean two different things which are very different but somehow connected.
The idea of symmetric encryption is that information is encrypted with a single "key" & the same "key" is used for decrypting the information also.
In asymmetric encryption, we have one key for encrypting information and another for decrypting it. Both the keys are completely different but are somehow related to each other (hence the word asymmetric). Now if you involve deep mathematical cryptographic functions to create these keys then you can call it asymmetric cryptography (also known as Public-key cryptography).
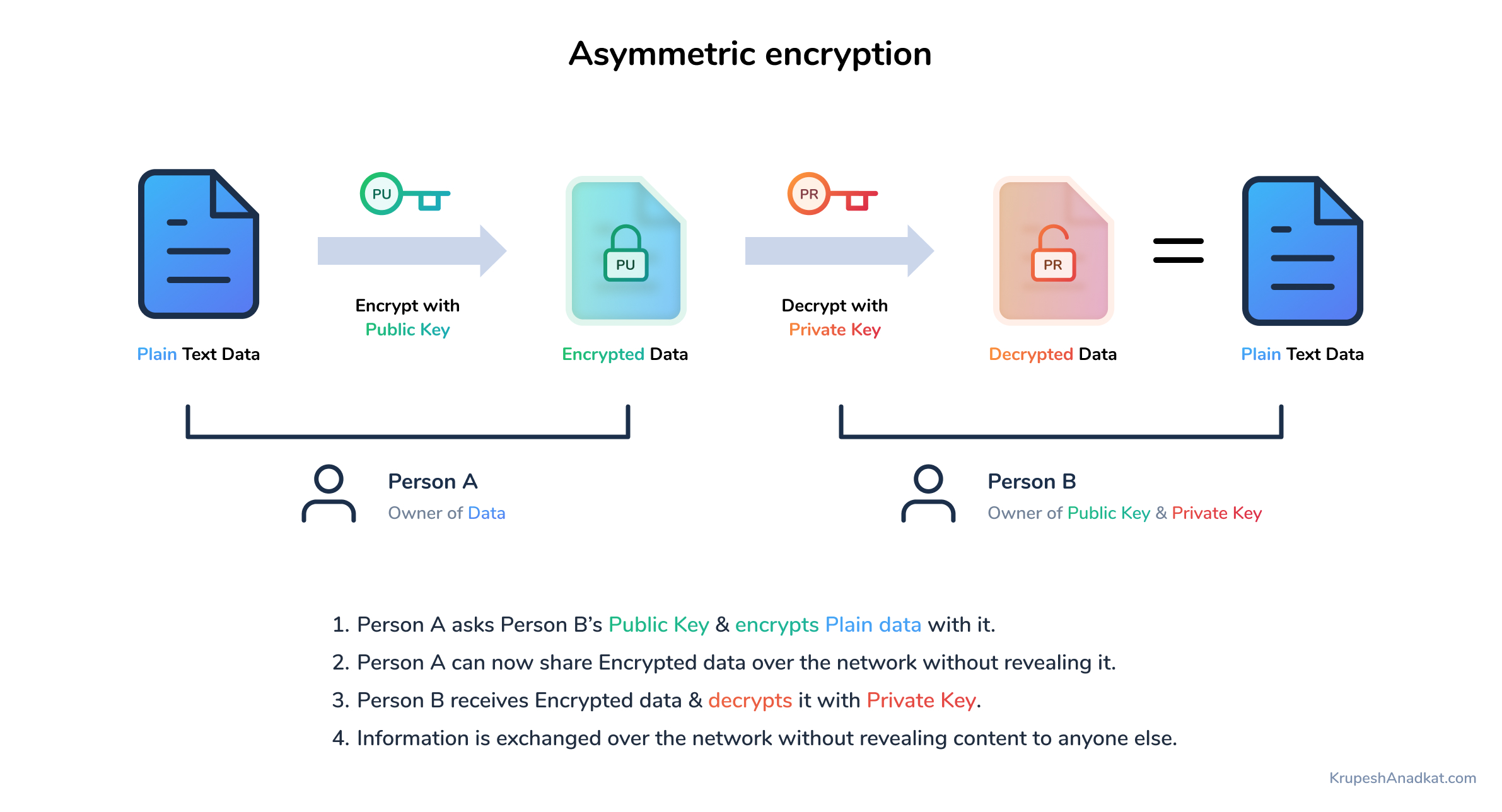
The above diagram demonstrates asymmetric encryption. Here Person A wants to send information to Person B but they want to keep it secret. They cannot trust the network for "Exchange of Information", asymmetric encryption at the rescue! Person B generates Public & Private keys using cryptography functions and shares the Public key with Person A. Person A encrypts the information with it and sends it to Person B via an untrusted network. Person B decrypts it using the Private key and reads the info, voila!
Public key as the name suggests, you could distribute copies of it to anyone interested in sending you encrypted information. Private key however should stay with you only - always.
Public key & Private key are generated in a pair and are mathematically connected! You cannot expect to generate several different public-private key pairs and interchange while using them. Every time you generate a new public-private key pair with cryptography functions, the pair is unique - it will never be the same as what you generated last time!
Performance & Threat Of Quantum Computers
Asymmetric encryption got prominent around the mid-1970s, before that cipher systems used symmetric encryption. The whole digital encryption stuff had come into existence way before I was born (1996). Asymmetric encryption has evolved since then with several algorithms and newer standards.
Compared to symmetric encryption, asymmetric encryption is rather slower than good symmetric encryption, too slow for many purposes. Today's cryptosystems (such as TLS, Secure Shell) use both symmetric encryption and asymmetric encryption.
As you can read above, asymmetric encryption has performance drawbacks. When we will write some code, you would notice it would take 0.5s to 1s to generate keys with larger bits (size). There is also a limitation on the number of characters or letters you can encrypt, if we have a larger key size, more characters can be encrypted & vice-versa.
Let's assume we are hackers, little not-so-smart hackers & we would want to somehow decrypt data without the private key. Well, one way could be we run a loop in which we create the private key and check if it decrypts the information and continue it for eternity (that is heck of a long time) given computational power current systems have. What if we got our hands onto Quantum Computers 👨🏻💻 They are factually proved to be so many times faster than regular multicore GPU systems.
The two best-known quantum computing attacks are based on Shor's algorithm and Grover's algorithm. Of the two, Shor's offers the greater risk to current security systems. Derivatives of Shor's algorithm are widely conjectured to be effective against all mainstream public-key algorithms including RSA, Diffie-Hellman and elliptic curve cryptography.
In short what we know is if sufficiently large quantum computers are built that could run a derivative of something called Shor's Algorithm, the complete security over the internet (banking, search engine results, information in public & government web servers) is no more trustworthy, they could be easily falsified or misused. It is scary, isn't it! Do not worry, they will come up with something else when the time comes :D
If you are curious, you could go ahead and read this: Post-quantum cryptography
The size of the key plays an important role in measuring how secure is the encryption. Restricting our discussion, as per the standard protocols keys generated by RSA should be equal to or more than 3072 bits for encryption/decryption & digital signatures.
Asymmetric Cryptography Algorithms
You would have noticed that till now we spoke about RSA a few times without mentioning what it is. For starters, RSA is the acronym for Rivest Shamir Adleman. These are the surnames of 3 people Ron Rivest, Adi Shamir and Leonard Adleman, who publicly described the algorithm in 1977.
The general idea of RSA algorithm is that two very large prime numbers are used to create Public Key & information is encrypted (transformed into cipher) with this key. Now anyone who knows these two prime numbers and could reverse the logical operation performed & could decrypt it. That's right, this information is stored in private key. Let us understand it with a very basic math problem analogy. Not at all complicated, just follow me.
Let us take two prime numbers 3 & 5. I want to send number 45 to my friend Bob in class. But I do not want anyone else to know this answer(45). I did the following:
45 / 5 => 9
9 * 3 => 27I sent number 27 to Bob. Before class started, Bob and I discussed in the recess that I will first divide the given number by 5 & then multiply the result by 3. After receiving 27 in a chit from me (cipher answer - fooling intermediary classmates who opened and saw the answer while passing chit 😄), Bob did the following:
27 / 3 => 9
9 * 5 => 4545. Aha! Bob has got the answer 45 which I originally intended to share. He reversed the calculation steps with prime numbers 3 & 5.
The above exercise would give you a very very remote idea of what the RSA algorithm does, what calculation to do & how to do it is all part of it. There is no need to go in-depth about this. Just know it is the mathematics involved to generate those keys.
There are several algorithms besides RSA for asymmetric encryption, just to name a few:
- Diffie–Hellman key exchange protocol
- Digital Signature Algorithm with DSS
- ElGamal
- Elliptic-curve cryptography
a. Elliptic Curve Digital Signature Algorithm (ECDSA)
b. Elliptic-curve Diffie–Hellman (ECDH)
c. Cramer–Shoup cryptosystem
Have these names in the back of your mind and you will good. In your free time and out of interest I would recommend reading about "Elliptic-curve cryptography". Not at all prerequisite to know all or any of these to move ahead in blockchain application development. If you have an idea then you would get a better intuition of what you are doing, that's it.
Conclusion
I know, you might want to code and see asymmetric encryption that too at production-grade, so that when you read WhatsApp mentioning "your chat is end to end encrypted..." you have an idea what happens behind the scenes & in case you want to add such encryption into your app you could do it, with confidence! Let us do this in part 2 of this article, where we will directly start coding, with this article as foundation theory. I hope you enjoyed this one & gained knowledge with clarity, see you next time!
